Haoyue Hu did her honours project at the Institute of Automotive Technology (TUM) and
was supervised by Dipl.-Ing. Thomas Hierlinger and Prof. Dr.-Ing. Markus Lienkamp.
Introduction
The electric vehicle MUTE [1] is developed and built at TUM since 2010. In a subsequent research project the MUTE shall be further improved. One goal is to achieve the best possible occupant safety with a total weight below 400 kg excluding the battery. In order to develop a light and safe vehicle, FEM software is extensively deployed to study the components’ load-carrying behavior. Closely related is structural optimization which plays a vital role in finding the optimal design under given constraints. In this project the seat is optimized with respect to minimum weight, under consideration of maximum loads during crash.
 |
 |
|
Fig.1: Exterior view of MUTE
|
Fig.2: Seat design
|
Crash Simulations
Crash simulations are carried out in LS-DYNA using explicit FEM to determine maximum loads acting on the seating structure. Sheet components like the seating area, backrest, and lumbar support are discretized with shell elements. The support structure is modeled with solid elements. For the shafts beam elements are used. The rigid dummy of type 95% Hybrid III is provided by LSTC.
Two crash cases are simulated, the front crash to achieve the maximum bearing reaction forces and the rear crash to determine the maximum load acting on the seat components caused by the dummy. The whole structure is subjected to an acceleration pulse as dynamic excitation.
 |
|
Fig.3: Crash model in LS-DYNA
|
Linear Static Optimization
Topology, size and shape optimization are conducted using OptiStruct. Worst-case static load cases are extracted from the crash simulations using MATLAB scripts. The objective is minimum weight and the constraints are von Mises stresses in all components that must not exceed a limit stress dependent on the material.
It is found that the initial design does not fulfill the given constraints and, thus, is not a valid design. Therefore, some sheets have to be reinforced. With size optimization, optimal sheet thicknesses and shaft sections are obtained. Since the shafts are mainly subjected to bending, hollow shafts are better suited than solid shafts, as shown in Fig.5. For the other solid components free shape optimization is performed. The position of surface nodes is varied in order to change the design in detail for better load-carrying behavior.
 |
 |
|
(a) Initial sheet thicknesses
|
(b) Optimized sheet thicknesses
|
 |
 |
 |
 |
|
(a) Initial shaft
|
(b) Final hollow shaft
|
(c) Final solid shaft
|
(d) Final solid shaft (ESLM)
|
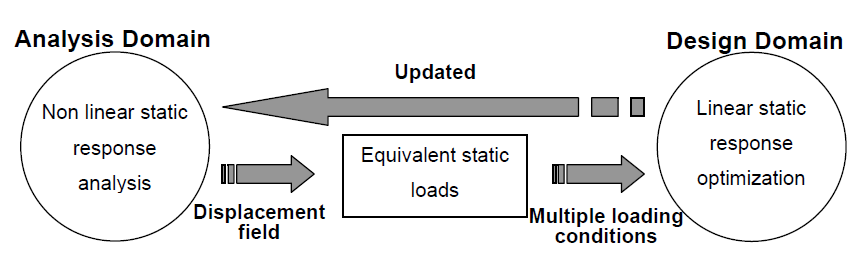
Nonlinear Dynamic Optimization Using the Equivalent Static Loads Method (ESLM)
The ESLM developed by Park [2] may be used for nonlinear and dynamic load cases. At each considered time step equivalent static loads are generated from nonlinear analysis that cause the same displacement field in linear analysis. With these loads, a linear static optimization is then performed. Afterwards, a nonlinear analysis is repeated with the updated design.
Conclusions
Using linear static topology, size, and shape optimization, the weight of the seating structure may be reduced by 11%, with the initial design as reference. Compared to a modified design that is able to withstand the static loads, a reduction of 23 % is achieved. Nonlinear dynamic optimization based on ESLM reveals further potential in weight reduction. A size optimization with ESLM shows that the design may be 18 % lighter compared to the initial one. For the ESLM, the obtained optimization results depend on the considered time steps. For a low number of time steps the load case cannot be represented properly whereas for many time steps the computation takes very long.
Linear static optimization is a well studied method and results in a safe design for maximum loads. The ESLM shows potential for further improvement, but it is more complex to use.
References
[1] www.mute-automobile.de
[2] Park, Gyung-Jin: Technical overview of the equivalent static loads method for non-linear static response structural optimization. In: Structural and Multidisciplinary Optimization 43 (2011), 3, p. 319-337.
