Jan Götz did his honours project at the Institute of Fluid Mechanics (LSTM) in Erlangen.
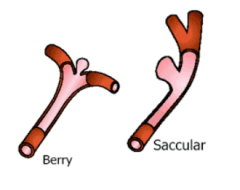Aneurysms in blood vesselsExperience at the Institute of fluid mechanics with pulsating flow simulations through blood vessels with aneurysms has shown that reliable results for periodically forced flows through complicated geometries with branches, cavities and bends can only be obtained on the basis of a preliminary computation of a time-independent incompressible velocity fields as initial condition. This field contains the complete influence of the geometry on the hemodynamics while the final solution includes also the effects of inertia and time-dependent forcing.
Lattice Boltzmann methods (LBM) have been shown to be very reliable in predicting steady incompressible flows through very complex geometries. But the convergence toward this solution is controlled by the explicit nature of LBM.
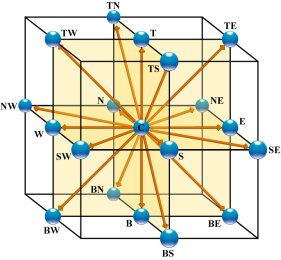Lattice Boltzmann discretisation of velocitiesFor a hemodynamics solver to be suited for routine application in clinical practice, the amount of computation required to obtain a converged solution must be reduced by orders of magnitude. One way towards this goal is to adapt multigrid (MG) methods, which have been developed for elliptic problems, to the present context of a hyperbolic dynamical system.
In the summer of 2004, a numerical and thorough theoretical investigation of this option has become available for the 2-D case. It indicates a unique optimal way of applying MG to LBM. This has to be now applied to the 3-D case. The effects of increasing geometry complexity and of the various LBM-specific boundary condition implementations need to be explored. The thereby chosen optimal algorithm will be eventually embedded into a LBM solver for hemodynamics in real, patient-specific vessel system geometries.