Yasunari Nishi did his Honour’s project at the Associate Professorship of Computational Mechanics (TUM)
supervised by Catharina Czech, M.Sc. and Prof. Dr.-Ing. habil. Fabian Duddeck.
The Finite Element (FE) simulations of natural fiber based materials such as wood is computationally very expensive due to the presence of material nonlinearities, geometrical nonlinearlities, and environmental influences. However, in the design process of the wodden structures, one may require optimization studies or uncertainty quantifications based on FE-analysis. Model Order Reduction (MOR) is a technique that allows us to reduce the complexity of the original numerical simulations by exploiting surrogate models, and it has been widely studied in the field of computational mechanics. This Honours project applies a data-driven MOR technique to the FE-simulations of wooden boards of European beech studied in [1] and aims to construct a simplified model of the original complex FE-simulations.
An overview of the problem description can be found in Figure 1. The dataset of fiber angles for European beech boards measured by multi-sensor scanners [1] and their FEM solutions for a tension experiment were made available by the professorship of wood technology (TUM). The resulting stress fields of FEM analysis are collected in a single large dimensional matrix called snapshot-matrix. Then, the snapshot-matrix is compressed into a smaller system via the singular value decomposition (SVD). The information of the fiber angle distribution are used as input for the training of a simplified model (surrogate model).
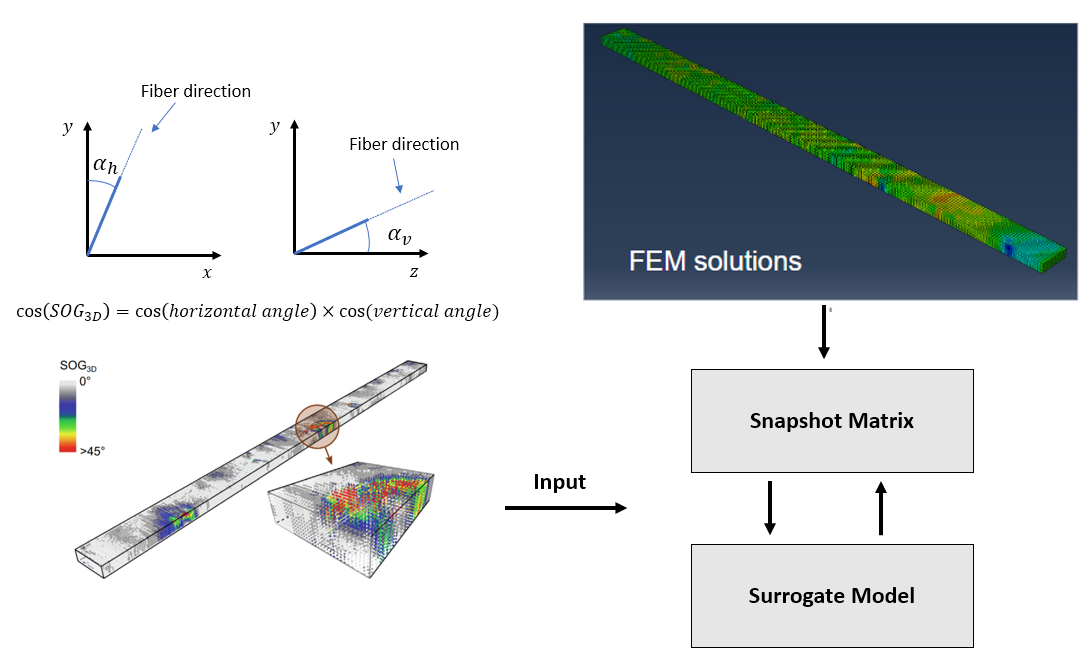
Fig. 1: Overview of the problem description. The figure of a scanned wooden board on the bottom left is taken from [1].
The mean and standard deviation of the 3D fiber angle are firstly used as input. The weights of the first 10 eigenmodes of the fiber covariance matrix are also considered to take into account the local distribution of the fiber angle. An exemplary comparison of the stress field from the FE-simulation and the one predicted by the reduced order model is shown in Fig. 2. Although the order of the stress is reasonable, the local values seem to be difficult to predict by the implemented method. Further studies using a random field approach [2] are planned to improve the prediction accuracy.
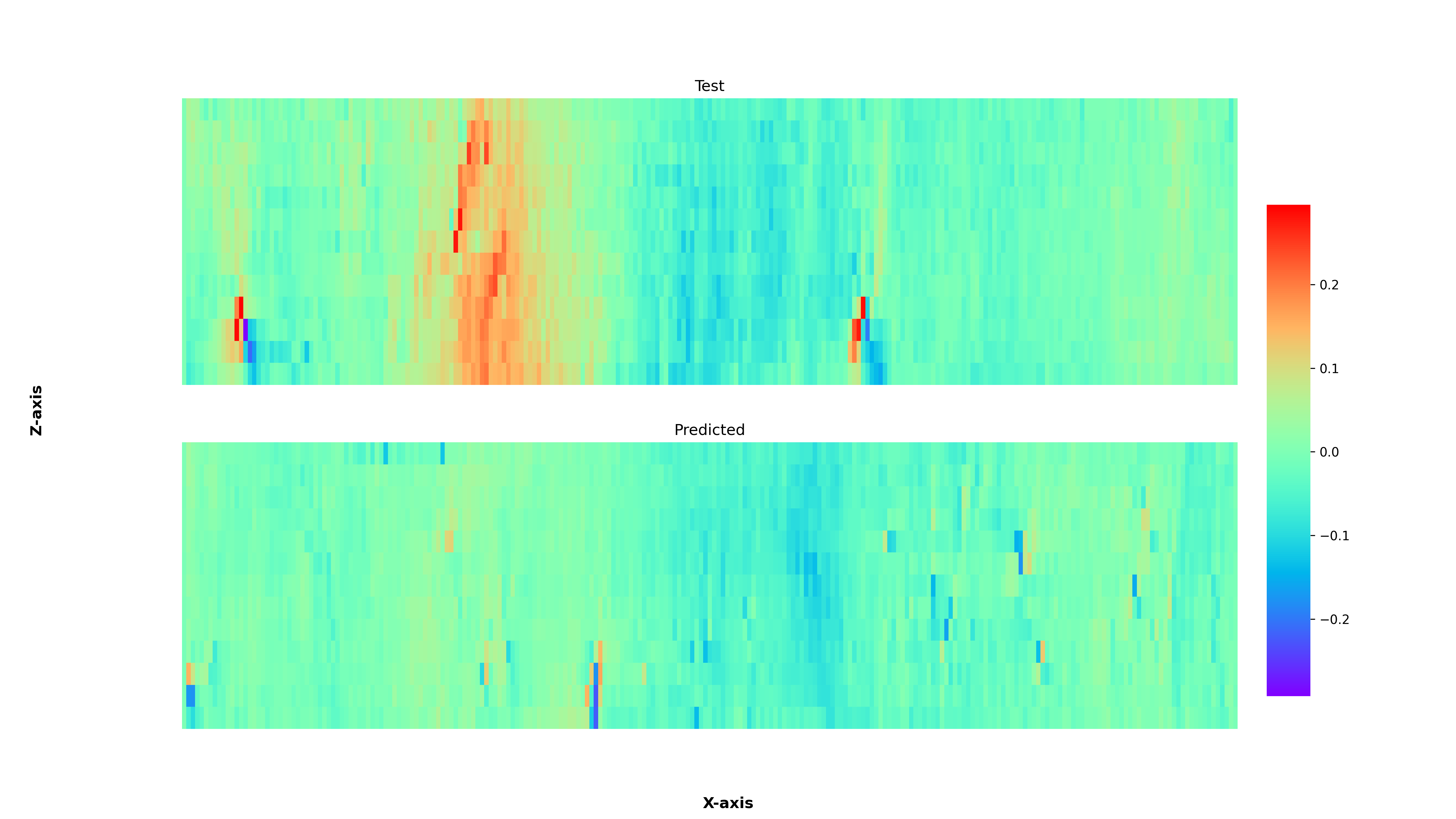
Fig. 2: Exemplary result for the comparison of the true stress field and the predicted stress field.
