Daniel Andres did his honours’ project at the Chair for Structural Analysis (TUM) and
was supervised by Philipp Bucher M.Sc., Suneth Warnakulasuriya M.Sc. and Rishith Ellath Meethal M.Sc.
Traditional computational methods face significant challenges with ever-increasing complexity in the problems of engineering interest. One set of problems that suffer from this phenomenon is those where Fluid-Structure Interaction (FSI) is present. FSI simulations are traditionally time-consuming and computationally expensive. Potential alternatives rely on using a surrogate model to substitute one or more systems involved. A promising approach employs artificial neural networks as the basis for such a surrogate combined with strong physics simulations based on finite element methods (FEM).
To implement such surrogate models, an integrated framework is required. The NeuralNetworkApplication from KratosMultiphysics was designed for this purpose [1] . In this project, the application is modified updated to enable the efficient simulation of surrogate models for FSI applications [2]. The additions in this project achieve a more modular design and enables future modifications.
Mok’s benchmark is chosen as the study case to test the capacity of the previous method applied to FSI (see Figure 1). In a first instance, the structural model in the example is substituted by a neural network-based model trained on known data while retaining the original fluid model. The neural networks have CNNLSTM architectures, that convine and Long-Short Term Memory layers. Additionally, a second case where a surrogate substitutes the fluid model, keeping the structural one untouched, is evaluated. In cases, the neural network predicts the total response of the system it substitutes. Strong and weak scenarios are considered. The results present improvements in simulation time without sacrificing especially when compared with the original benchmark. Weak coupling models (Figure 2) generally provide better accuracy at the expense of longer simulation times, while the strong coupling ones (Figure 3) significantly faster simulations with a negligible loss of accuracy.
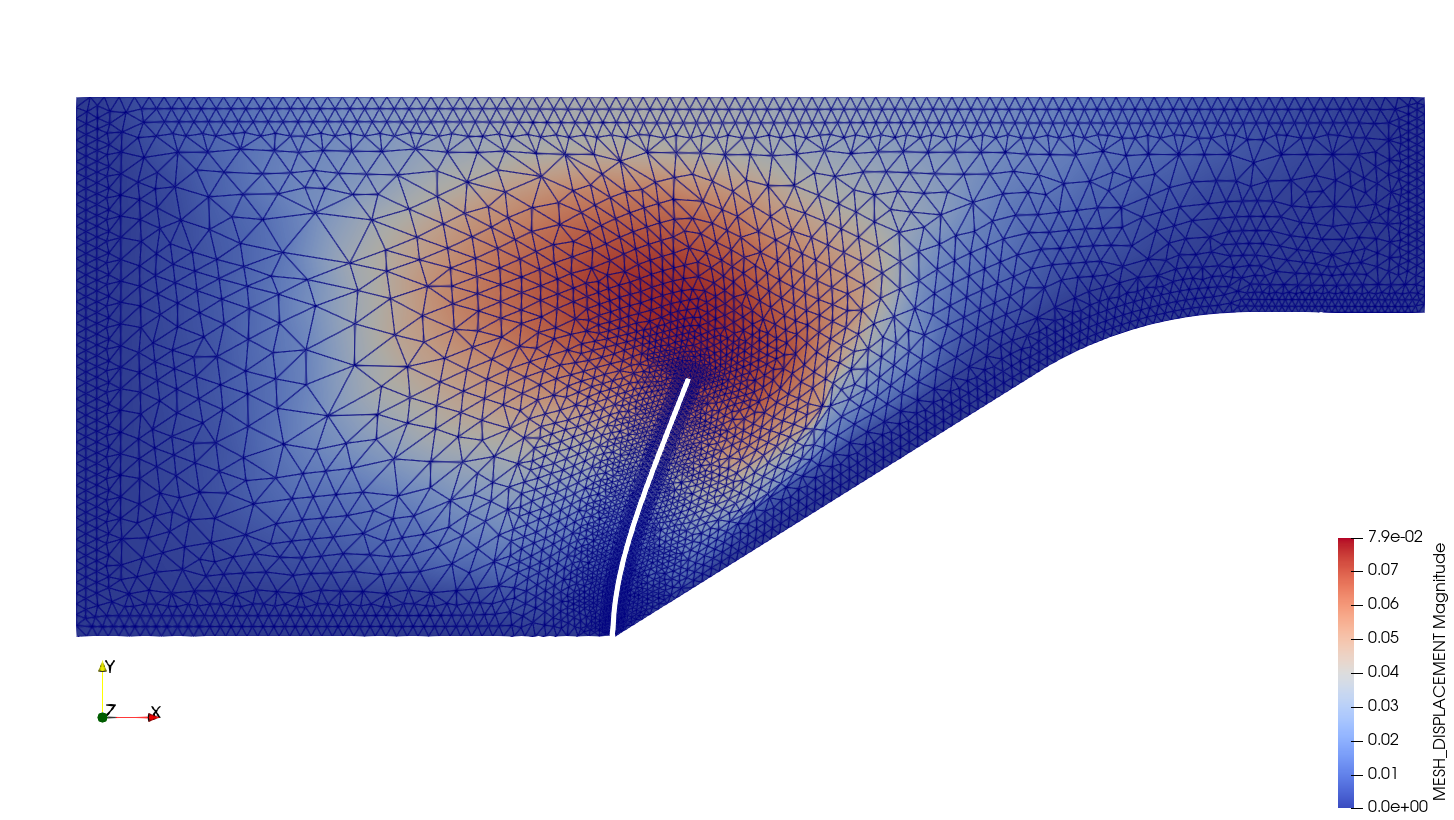
Fig. 1: Mok’s benchmark at t=100s.
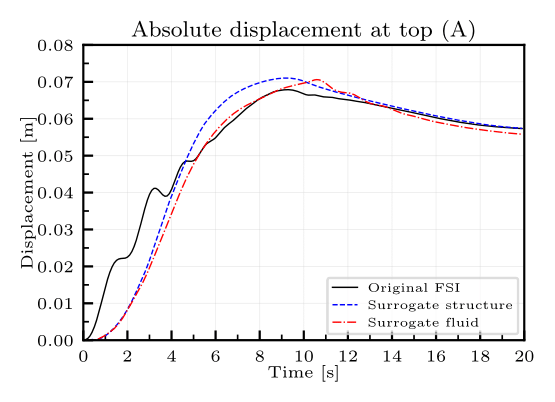
Fig. 2: Displacements at top of the structure under weak coupling.
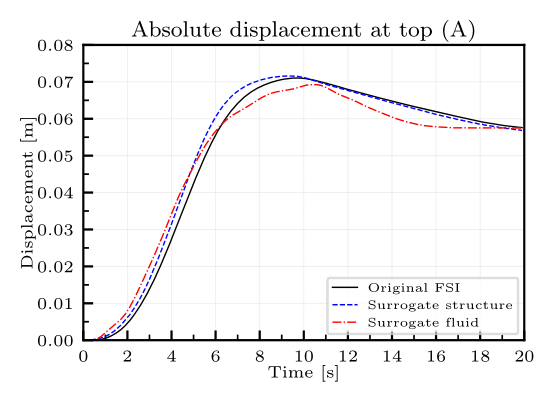
Fig. 3: Displacements at top of the structure under strong coupling.
